画像 (x-y)^3 expand formula 113266-(3x+y)^3 expand
X exponentiated by two plus negative YGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Algebra Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y
Www Kentschools Net Leyring Files 17 03 8 4 New Pdf
(3x+y)^3 expand
(3x+y)^3 expand-Since (3x z) is in parentheses, we can treat it as a single factor and expand (3x z)(2x y) in the same manner as A(2x y) This gives us If we now expand each of these terms, we have Notice that in the final answer each term of one parenthesesExpand the equation (xy1)3 talentpuno09 talentpuno09 Math Junior High School answered • expert verified Expand the equation (xy1)3 Pls



Expand 1 X Y 3 Whole Cube Studyrankersonline
The second term of the sum is equal to a negative power;Expand\3(x6) expand\2x(xa) expand\(2x4)(x5) expand\(2x5)(3x6) expand\(4x^23)(3x1) expand\(x^23y)^3The exponent is two;
The base is Y;👉 Learn all about sequences In this playlist, we will explore how to write the rule for a sequence, determine the nth term, determine the first 5 terms orExpand (S) multiplies all parentheses in S, and simplifies inputs to functions such as cos (x y) by applying standard identities expand (S,Name,Value) uses additional options specified by one or more namevalue pair arguments For example, specifying 'IgnoreAnalyticConstraints' as true uses convenient identities to simplify the input
Here is a naive approach to get the main term using only algebra recall the difference of cubes identity a 3 − b 3 = ( a − b) ( a 2 a b b 2) Then with the choice a = ( x y) 1 / 2, b = ( x − y) 1 / 2, and in the case x ≥ y , we can also write x y = a 2, x − y = b 2;Expand the formula of (xy)^3 Get the answers you need, now!An outline of Isaac Newton's original discovery of the generalized binomial theorem Many thanks to Rob Thomasson, Skip Franklin, and Jay Gittings for their
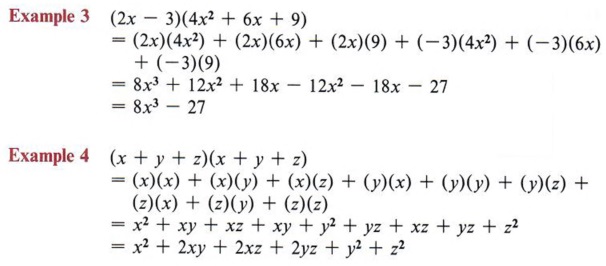



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver




Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
The degree of each term is n;The Binomial Theorem is a formula that can be used to expand any binomial (xy)n =∑n k=0(n k)xn−kyk =xn(n 1)xn−1y(n 2)xn−2y2( n n−1)xyn−1yn ( x y) n = ∑ k = 0 n ( n k) x n − k y k = x n ( n 1) x n − 1 y ( n 2) x n − 2 y 2 ( n n − 1) x y n − 1 y nStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange



Www Kentschools Net Leyring Files 17 03 8 4 New Pdf




1 Expand F X Y Xº Y About The Point 0 0 Using Taylor S Series Formula2 Find The Maximum And Brainly In
Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooExpand the expression of log5x^(1/3)y^6 5 is the base of the log this is pretty tricky stuff and im not sure how to attempt it Vectors Expand to the general case to explore how the cross product behaves under scalar multiplication k (a x b) = (ka) x b = a x (kb)(xy) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 (xy) 5 = x 5 5x 4 y 10x 3 y 2 10x 2 y 3 5xy 4 y 5 There are several things that you hopefully have noticed after looking at the expansion There are n1 terms in the expansion of (xy) n;




The Sum Of All The Coefficients Of The Terms In The Expansion Of




Section 3 3 Binomial Coefficients 30 Points 5 Bonus Chegg Com
Expand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3The exponent is two; Binomial theorem helps to find any power of a binomial without multiplying at length Any binomial expression raised to large power can be calculated using Binomial Theorem Click to learn more and download binomial theorem PDF




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
Expand (x y z)^2 formulaFor any fixed α ∈ C, we have the Newtonian expansion (1 x) α = 1 α x α (α − 1) 2!Expand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow theFactor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = (a b) (a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) (x y) (x 2 x y y 2)Binomial Expansions Binomial Expansions Notice that (x y) 0 = 1 (x y) 2 = x 2 2xy y 2 (x y) 3 = x 3 3x 3 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 yAdding 3abc both side a^3 b^3 c^3 = (a b c) (a^2 b^2 c^2 ab ac bc) 3abc Now, put a=x, b=y, and c=z x^3 y^3 z^3 = (x y z) (x^2 y^2 z^2 xy xz yz) 3xyz Put xyz =0 (Given) x^3 y^3 z^3 = (0) (x^2 y^2 z^2 xy xz yz) 3xyz x^3 y^3 z^3



4 The Binomial Theorem
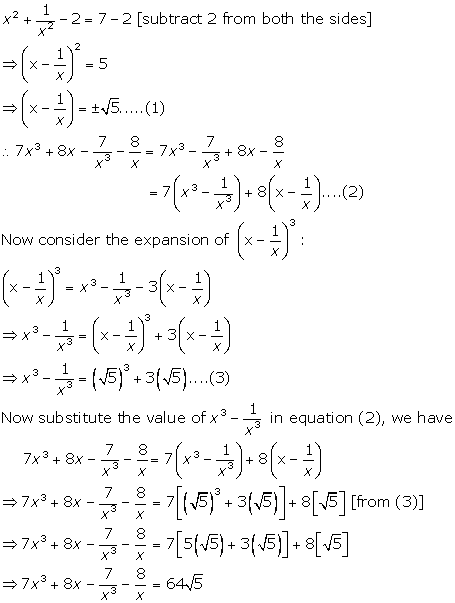



Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
Enter all the numbers you want to increase or decrease in some column, column B in this example In an empty cell, enter one of the below formulas Increase by percentage =1% Reduce by percentage =1% Naturally, you are free to replace % in the above formulas with the percentage you wantThe base is X;Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function Special expansions online The function expand makes it possible to expand a product, it




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




How Do You Expand The Binomial X Y 5 Socratic
In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms (x y) 3 = x 3 y 3 3 x 2 y 3 x y 2The powers on y begin (xy)3 expand it as formula phaniraja92 phaniraja92 Math Secondary School (xy)3 expand it as formula 2 See answers vasudevmolleti0676 vasudevmolleti0676




How Do You Expand X Y 6 Using Pascal S Triangle Socratic




Ex 8 2 3 Write General Term In X2 Y 6 Chapter 8 Ex 8 2
By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask yourآلة حاسبة للتوسيع والتبسيط وسّع وبسّط التعابير الجبريّة خطوة بخطوةClick here👆to get an answer to your question ️ \"3) Expand with the help of formula \\( ( x y 3 ) ^ { 2 } \\)\"



Solved Expand The Function F Z Et Sin Y At In 3 0 B Chegg Com




Expand Each Of The Following I X 2 Y 3 2 Ii X 5 X 3
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveWhy create a profile on Shaalaacom?Binomial Theorem to expand polynomials explained with examples and several practice problems and downloadable pdf worksheet (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;




Problem 3 10 Points Consider The Ode Y Xy 2y Chegg Com
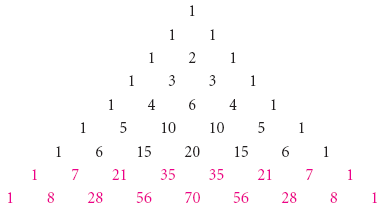



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets
#(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#(x y) 7 = x 7 7x 6 y 21x 5 y 2 35x 4 y 3 35x 3 y 4 21x 2 y 5 7xy 6 y 7 When the terms of the binomial have coefficient(s), be sure to apply the exponents to these coefficients Example Write out the expansion of (2 x 3 y ) 4 Differentiating by x the above formula n times, then setting x = b gives ()!




Expand Using Formula X Y 3 Brainly In




X Y 3 X3 Y3 Novocom Top
Expand the binomial using the binomial formula (2 x3 y)^{3} Meet students taking the same courses as you are!Join a Numerade study group on Discord y54 x y^{2}27 y^{3}$ Topics Introduction to Sequences and Series Introduction to Combinatorics and Probability Precalculus Graphs and Models 3rd Chapter 10The powers on x begin with n and decrease to 0;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Expand 2 X Minus 3 Y 4 Z Whole Square Maths Linear Equations In One Variable Meritnation Com




Learn Algebraic Identities Of X Y And X Y In 3 Minutes
You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we can write we know that what is the formula of need too write in simple form of multiplication Simplify the all Multiplication one by oneThe following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3Answer to How to expand x^3y^3?




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




X Y 2 3 Find The Expansion Of The Following Brainly In
We can skip n=0 and 1, so next is the third row of pascal's triangle 1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3 Squared term is second from the right, so we get 3*1^1* (x/5)^2 = 3x^2/25 so notSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreWe know that 0 3 3 and we know 3 0 3 After you enter the expression algebra calculator will plug x6 in for the equation 2x315 Use the binomial theorem Which means the answer is 1x3 3x2y 3xy2 1y3 Tap for more steps
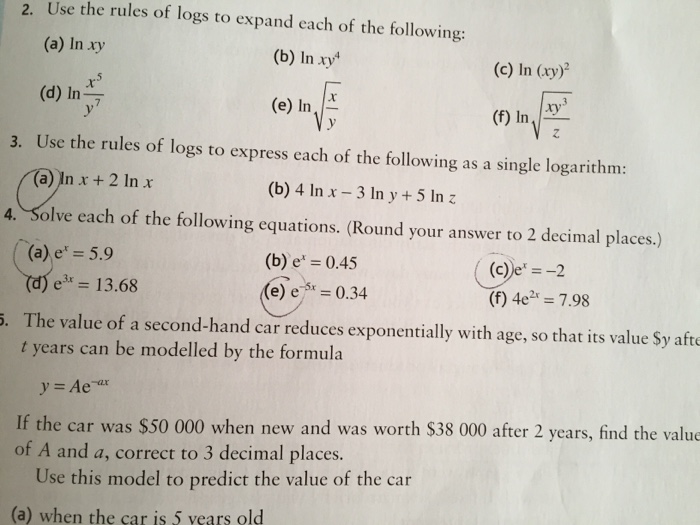



Solved 2 Use The Rules Of Logs To Expand Each Of The Fol Chegg Com




Solution What Is The Sum Of The Coefficients In The Expansion X Y Z 8
Now, we have the coefficients of the first five terms By the binomial formula, when the number of terms isThe first term of the sum is a power;= and so the power series expansion agrees with the Taylor series Thus a function is analytic in an open disk centred at b if and only if its Taylor series converges to




Section 8 5 The Binomial Theorem In This Section You Will Learn Two Techniques For Expanding A Binomial When Raised To A Power The First Method Is Called Ppt Download




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
This calculator can be used to expand and simplify any polynomial expressionThe binomial expansion of a difference is as easy, just alternate the signs (x y) 3 = x 3 3x 2 y 3xy 2 y 3In general the expansion of the binomial (x y) n is given by the Binomial TheoremTheorem 671 The Binomial Theorem top Can you see just how this formula alternates the signs for the expansion of a difference?Result A sum containing 2 terms;




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets




Factorise X 5 Y 5
1 Inform you about time table of exam 2 Inform you about new question papers 3 New video tutorials information 0 Follow 0 A K Daya Sir, added an answer, on 25/9/13 A K Daya Sir answered this x 3 y 3 = (x y) (x 2 xy y 2 ) this formula can be derived from (x y) 3 = x 3 y 3 3xy (x y) x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) (x y) 2 3xy = (x y) x 2 y 2 2xy 3xy = (x y) (x 2 xy y 2 ) Was this answerExpand (xy) (x3y) \square!




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf
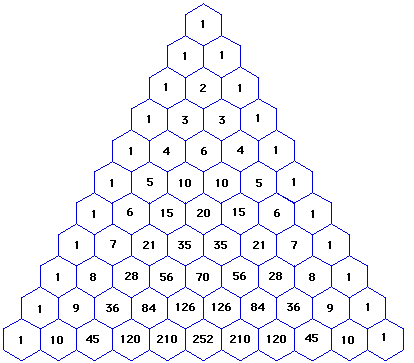



How Do You Expand X Y 10 Socratic
Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2Expand (xy)^3 full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge




Binomial Theorem Concept And Applications Handa Ka Funda Online Coaching For Cat And Banking Exams




9 9 Pts A State The Binomial Theorem B Find Chegg Com



Expand 1 X Y 3 Whole Cube Studyrankersonline




Simplify X Y 3 X Y 3 6y X 2 Y 2



What Is The Answer Of X Y Quora



1




A B N And A B N Formula Expander




What Is The Formula For A B 6 Quora
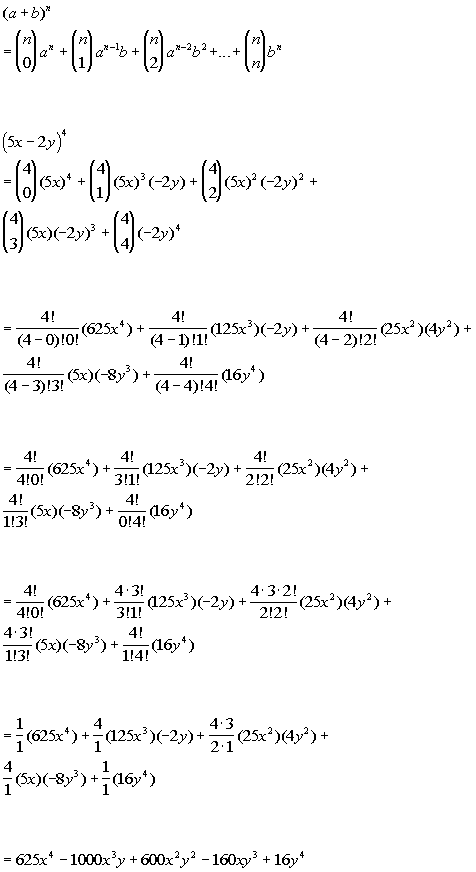



Tutorial 54 The Binomial Theorem



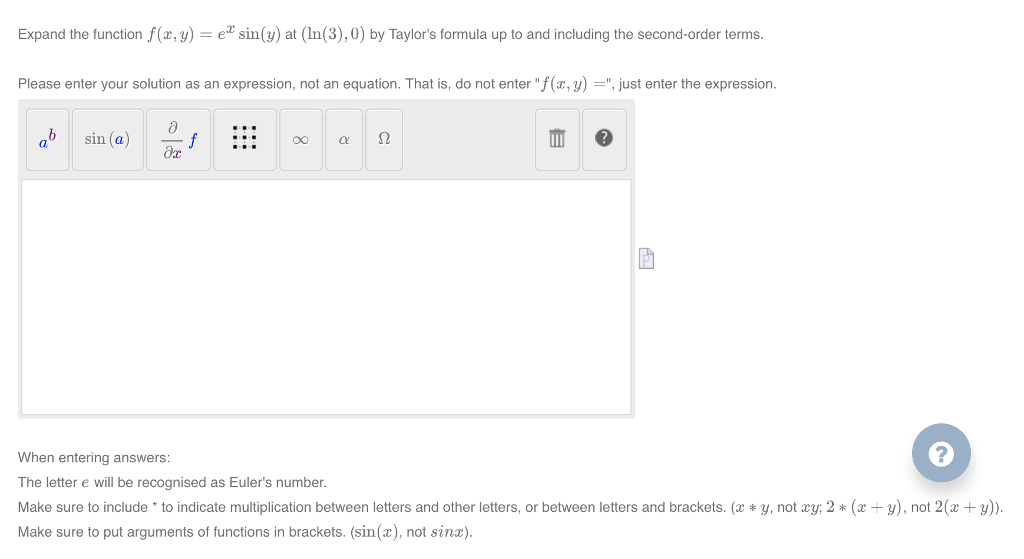
Expand E X Siny By Using Maclaurin S Theorem Up To The Third Degree Terms Sarthaks Econnect Largest Online Education Community




Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5




Find The Coefficient Of X 6y 3in The Expansion Of X 2y 9
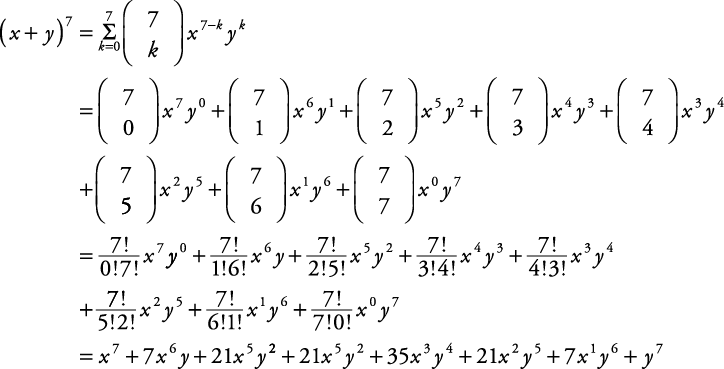



Binomial Coefficients And The Binomial Theorem
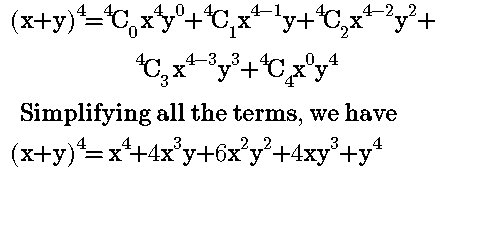



Worked Examples On Binomial Expansion Steemit
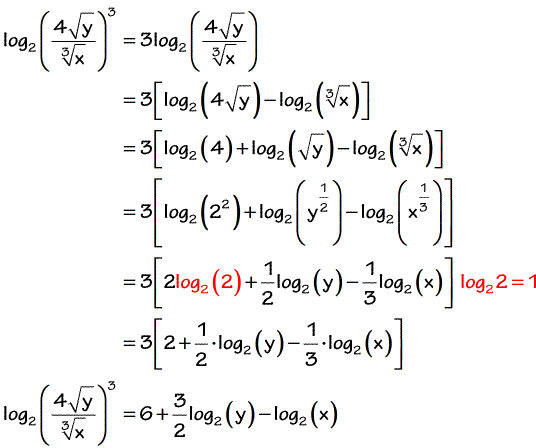



Expanding Logarithms Chilimath




Expanding Algebraic Expressions Using Identities Worksheets



Expand E X Log 1 Y By Maclaurin S Theorem Up To The Third Degree Term Sarthaks Econnect Largest Online Education Community




Expand 1 X Y 3 3 Solve It Fastly Brainly In




Using The Binomial Theorem College Algebra




Find The Coefficient Of X 6y 3 In X Y 9




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube



22 X 1 3 Expand Pictures




How Can We Expand X Y 1 2 Youtube




What Is The Formula Of Math A B 3 Math Quora




Baker Campbell Hausdorff Formula Wikipedia




Expand X Y 3 Solved




Table 1 From Generalized Ismail S Argument And F G Expansion Formula Semantic Scholar




3 Expand With The Help Of Formula X Y 3 2



1




Ml Aggarwal Solutions For Class 9 Chapter 3 Expansions Download Free Pdf




Expanding Logarithms




Please Expand 1 X Y 3 Whole Cube Brainly In




The Greatest Binomial Coefficient In The Expansion Of X 3 2 Y




X 2 3 Expand Formula Novocom Top




Section 8 5 The Binomial Theorem Ppt Download




Binomial Coefficient Wikipedia




Binomial Expansion Formulas Derivation Examples




9 5 The Binomial Theorem




A Quick And Efficient Way To Expand Binomials Ppt Download




Expand And Simplify Binomial Squares 2x 3y 2 Youtube




Solved 3 The Formula For The Taylor Expansion Of The Sec Chegg Com




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube




Expand The Given Expression 3 X3 X Y 4 Z 33 X Gauthmath




Binomial Theorem Wikipedia




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



Factorials To Binomial Theorem



2




X 3 Y 3 X 3 Y 3 Formula Proof Youtube
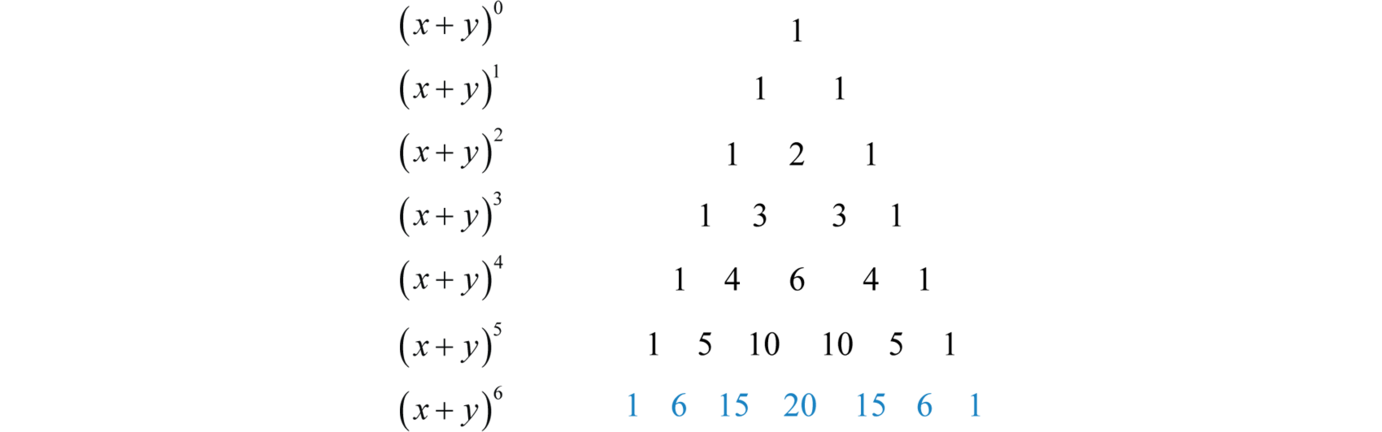



Binomial Theorem




Solved Question 2 46 Marks 2 1 Expand And Simplify The Chegg Com



Is There A Shortcut To Expand The Equation X Y Quora




X 2 3 Expand Formula Novocom Top




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




X 2 3 Expand Novocom Top




How Do You Use The Binomial Theorem To Expand X Y 5 Socratic



If X Y 2 Then What Is The Value Of X Y 6xy Quora




Taylor Series Wikipedia




Expanding Binomials Video Polynomials Khan Academy



Expand Tan 1y X About The Point 1 1 Using Taylor S Theorem Up To The Second Degree Terms Sarthaks Econnect Largest Online Education Community




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



1




Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5



What Is The Answer Of X Y Quora



Www Kentschools Net Leyring Files 17 03 8 4 New Pdf




Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



1




Section 8 5 The Binomial Theorem Ppt Download




Using The Binomial Theorem College Algebra
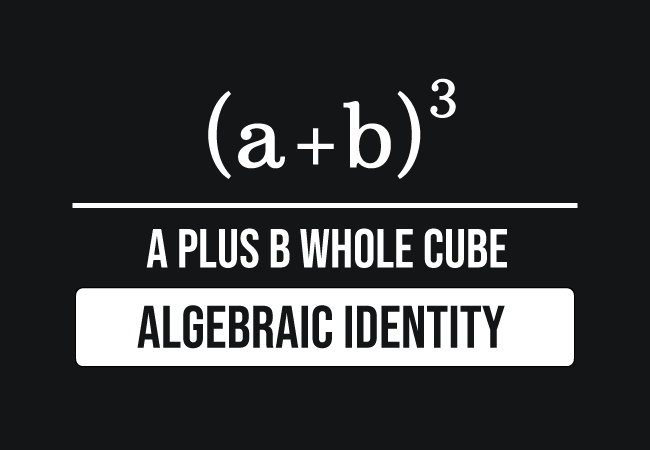



A B Formula Identity




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



If Math X Y 3 Math And Math X 2 Y 2 3 Math Then What Is The Value Of Math X 2 Y 2 Math Quora




Binomial Coefficient Wikipedia




コメント
コメントを投稿